十进制不够看：网络世界的二进制与十六进制大解密

进制转换是数学与计算机科学中的基础概念，它在理解数字系统和数据表示中起着至关重要的作用。从十进制到二进制、十六进制，不同的进制系统有其特定的应用场景，如在网络通信中的IP地址和MAC地址表示。本文旨在详细探讨这些进制系统及其在网络标识中的应用。

 思科认证 | 华为认证 | IT技术 | 网络工程师 

 3000人技术交流QQ群 备注【官网】更快通过 

十进制系统，作为我们最熟悉的数字系统，是基于10的逢十进一原则。例如，数字123可以表示为1100 + 210 + 3*1 = 100 + 20 + 3 = 123。这种系统适用于日常计算和大部分数学运算。 

相比之下，二进制系统则基于2，即逢二进一。在二进制中，每个位的值是2的幂次方，从右到左依次增加。例如，二进制的1111可以转换为十进制的2^7 + 2^6 + 2^5 + 2^4 + 2^3 + 2^2 + 2^1 + 2^0 = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255。二进制系统是计算机科学中的基本工具，因为计算机内部处理的是开/关状态，这可以直接对应到二进制的0和1。

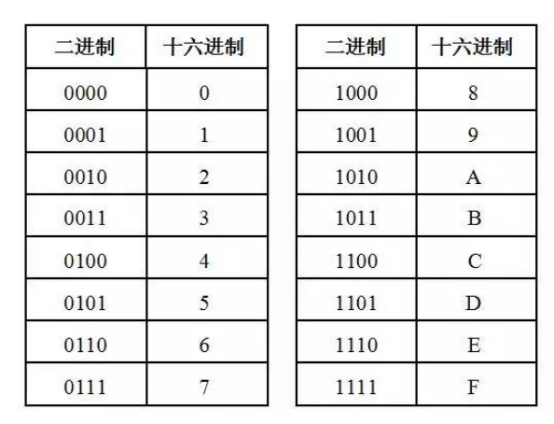
进一步地，十六进制系统则是逢十六进一，它使用0到9和A到F来表示数值，其中A到F分别代表10到15。这种系统在编程和网络地址（特别是MAC地址）的表示中非常有用。

在网络通信领域，这两种进制系统的应用尤为重要。IP地址，用于识别网络上的设备，通常以十进制表示，范围从0.0.0.0到255.255.255.255。这个范围是通过将IP地址的每个段视为一个0到255的数字来得到的，对应于二进制中每个段的8位。 

理解这些进制之间的转换不仅有助于我们更好地理解计算机和网络技术，而且对于网络安全也至关重要。例如，通过分析IP和MAC地址，我们可以进行网络监控，检测未授权设备或潜在的安全威胁。

总之，进制转换是理解和应用数字技术的关键，无论是在数据处理还是在网络通信中，都有其不可替代的地位。掌握这些基本概念，可以帮助我们更好地理解复杂的技术概念，并在实际应用中发挥其价值。